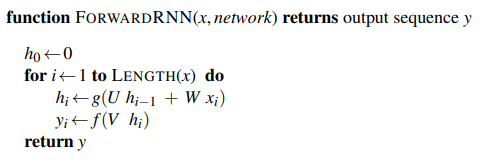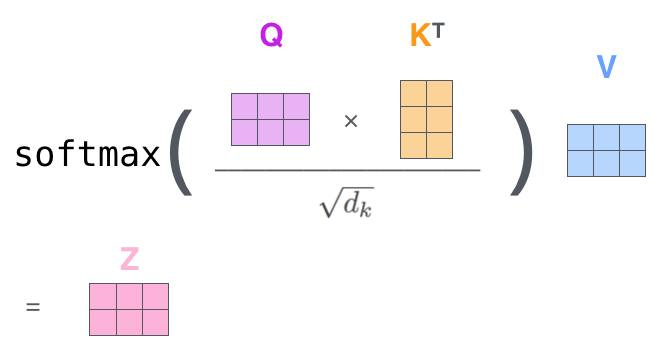Plan¶
- Sztuczne sieci neuronowe
- Algorytm wstecznej propagacji błędu
- Sieci rekurencyjne
- Komórka LSTM
- Sieci transformacyjne
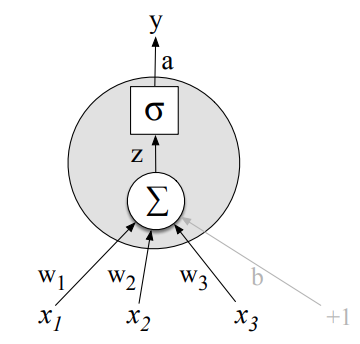
$$
z = w \cdot x + b
$$
$$
y = a = f(z)
$$
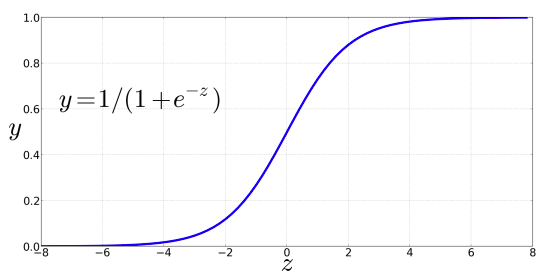
$$
\sigma(z) = \frac{1}{1 + e^{-z}}
$$
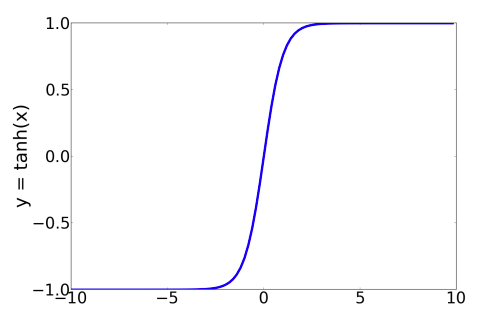
$$
tanh(z) = \frac{e^z - e^{-z}}{e^z+e^{-z}}
$$
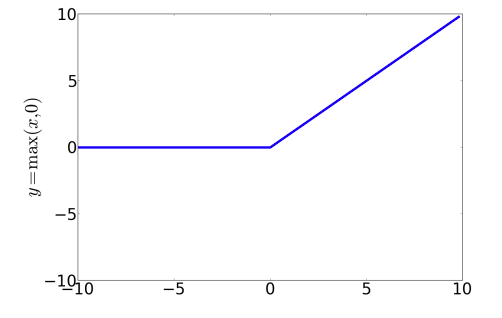
$$
ReLU(z) = max(x, 0)
$$
$$
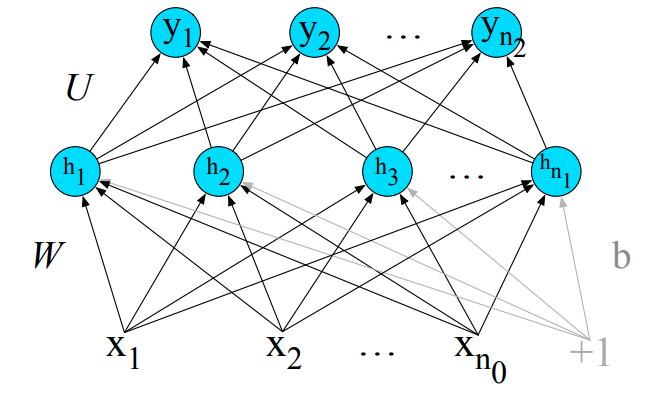
h = f(Wx + b)
$$
$$
x \in R^{n_0}
$$$$
h \in R^{n_1}
$$$$
b \in R^{n_1}
$$$$
W \in R^{n_0 \times n_1}
$$
$$
z = Uh
$$
$$
\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^d e^{z_j}}
$$
Uogólniona notacja¶
$$ \begin{split} a^{[0]} & = x\\ z^{[1]} & = W^{[1]}a^{[0]} + b^{[1]}\\ a^{[1]} & = g^{[1]}\left(z^{[1]}\right)\\ \end{split} $$
$$
\begin{split}
z^{[2]} & = W^{[2]}a^{[1]}+b^{[2]}\\
a^{[2]} & = g^{[2]}\left(z^{[2]}\right)\\
\hat y & = a^{[2]}
\end{split}
$$
$$
\begin{split}
z^{[i]} & = W^{[i]}a^{[i-1]} + b^{[i]}\\
a^{[i]} & = g^{[i]}\left(z^{[i]}\right)
\end{split}
$$
Funkcja straty (loss function)¶
$$
L_{CE}(\hat y,y) = - \sum_{i=1}^{C} y_i log\hat y_i
$$
$$
L_{CE}(\hat y,y) = - log \hat y_i
$$
$$
L_{CE}(\hat y,y) = \frac{e^{z_i}}{\sum_{j=1}^{C} e^{z_j}}
$$
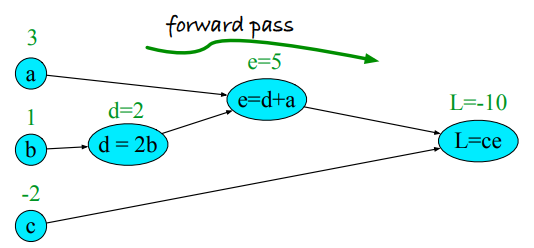
$$
\begin{split}
d & = 2 * b\\
e & = a + d\\
L & = c * e
\end{split}
$$
Plan¶
- Sztuczne sieci neuronowe
- Algorytm wstecznej propagacji błędu
- Sieci rekurencyjne
- Komórka LSTM
- Sieci transformacyjne
Wsteczna propagacja błędu (error backpropagation, backprop)¶
$$
f(x) = u(v(x))
$$
$$
\frac{df}{dx} = \frac{du}{dv}\cdot\frac{dv}{dx}
$$
$$
\frac{\partial L}{\partial a}, \frac{\partial L}{\partial b}, \frac{\partial L}{\partial c}
$$
$$
\frac{\partial L}{\partial c} = e
$$
$$
\begin{split}
\frac{\partial L}{\partial a} & = \frac{\partial L}{\partial e}\frac{\partial e}{\partial a}\\
\frac{\partial L}{\partial b} & = \frac{\partial L}{\partial e}\frac{\partial e}{\partial d}\frac{\partial d}{\partial a}
\end{split}
$$
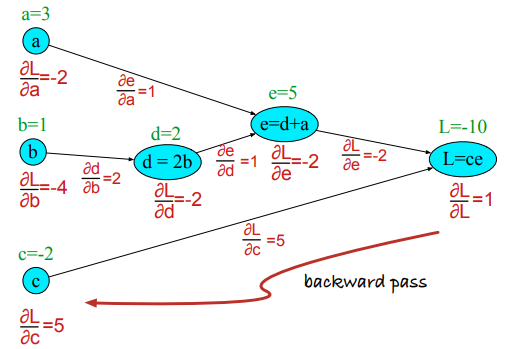
$$
\begin{split}
L = ce & : \frac{\partial L}{\partial c}=e,\frac{\partial L}{\partial e}=c\\
e = a+d & : \frac{\partial e}{\partial a} =1,\frac{\partial e}{\partial d}=1\\
d = 2b & : \frac{\partial d}{\partial b}=2
\end{split}
$$
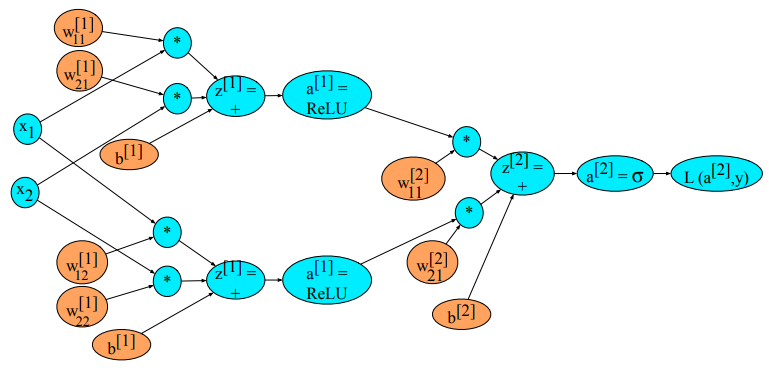
Proces uczenia¶
- stała ucząca/szybkość uczenia się (learning rate)
- inicjalizacja wag
- mini-batch
- epoki
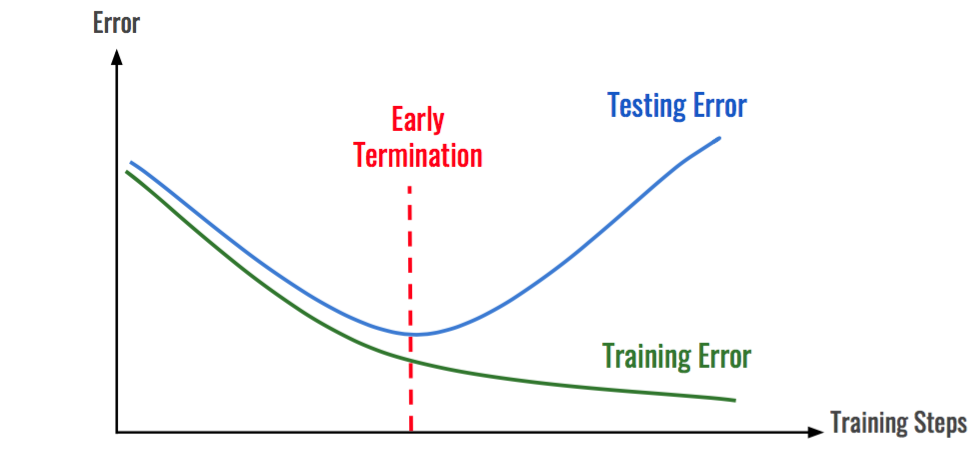
- wczesne zatrzymanie (early stopping)
- dropout
- algorytm optymalizacji
- optymalizacja hiperparametrów
- rola zbioru walidacyjnego
- środowiska do obliczeń: PyTorch, TensorFlow, Jax
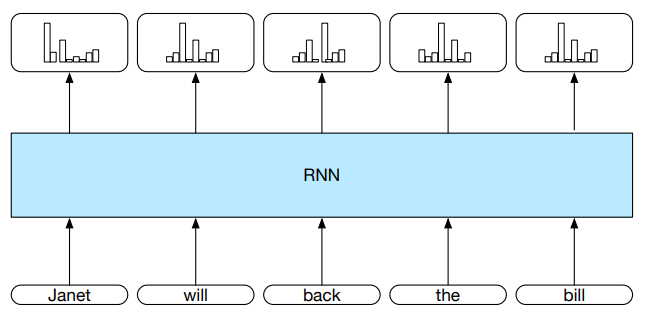
Kluczowy problem - sekwencyjna natura tekstu¶
- Proste modele, jak bag-of-words nie nadają się do klasyfikacji tokenów
- Modele takie jak HMM, MEMM są ograniczone jeśli chodzi o reprezentację kontekstu:
- kontekst jest niewielki: 2-3 tokeny
- cechy są określane manualnie
- Zależności w tekście mogą być długodystansowe
- Gdybym wiedział wtedy to co wiem dzisiaj, to bym się nie ...
- Gdybym wiedziała wtedy to co wiem dzisiaj, to bym się nie ...
Plan¶
- Sztuczne sieci neuronowe
- Algorytm wstecznej propagacji błędu
- Sieci rekurencyjne
- Komórka LSTM
- Sieci transformacyjne
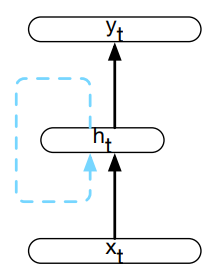
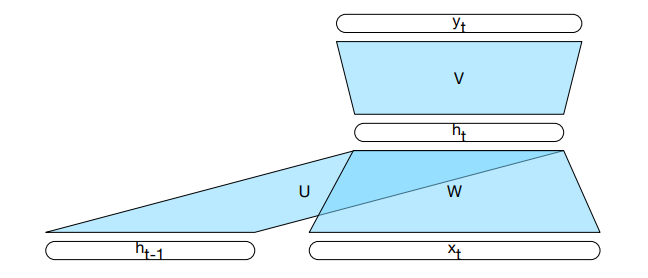
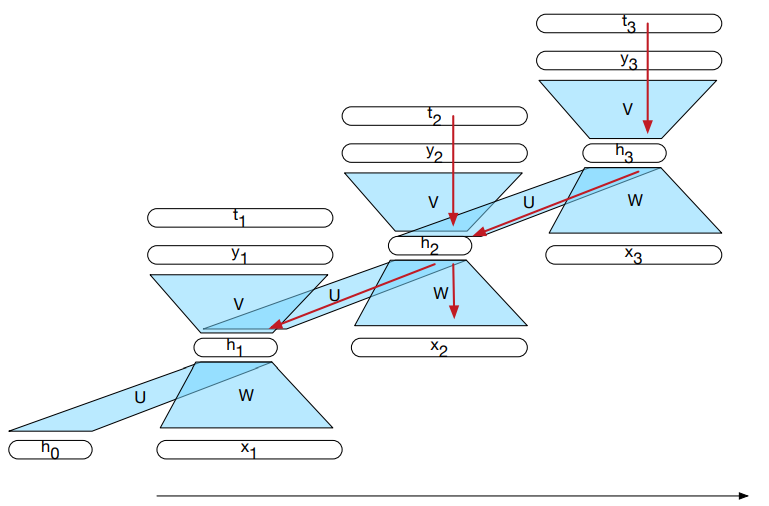
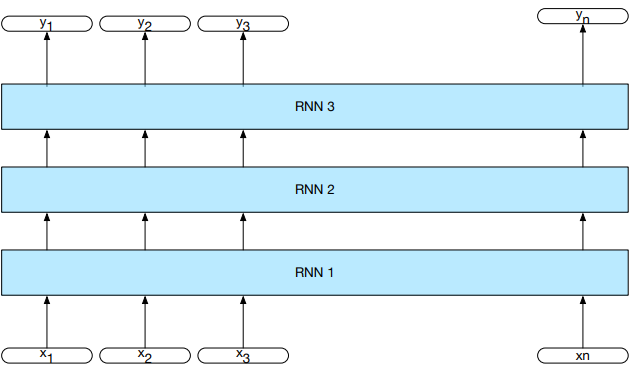
$$
h_t = g(U h_{t-1} + W x_t)
$$
$$
y_t = f(V h_t)
$$
Najczęściej f to funkcja softmax:
$$ \text{softmax}(\mathbf{y})_{i,t} = \frac{e^{y_{i,t}}}{\sum_{j=1}^K e^{y_{j,t}}} $$
$$
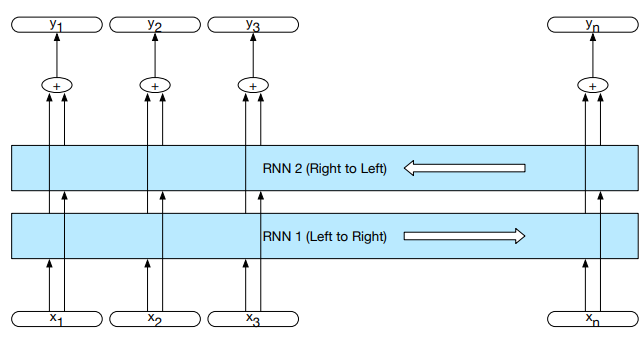
h_t^f = RNN_{forward}(x_1^t)
$$
$$
h_t^b = RNN_{backward}(x_t^n)
$$
$$
h_t = h_t^f \oplus h_t^b
$$
Sieć z długą pamięcią krótkoterminową (LSTM)¶
- informacja rozbita jest na dwie części:
- kontekst
- stan ukryty
- składa się z bramek
- struktura bramki:
- feed-forward
- funkcja sigmoidalna
- iloczyn punktowy
- typy bramek:
- zapominająca
- dodająca
- wyjściowa
Plan¶
- Sztuczne sieci neuronowe
- Algorytm wstecznej propagacji błędu
- Sieci rekurencyjne
- Komórka LSTM
- Sieci transformacyjne
Bramka zapominająca¶
- definiowana przez dwie macierze: $U_f$, $W_f$
$$
f_t = \sigma(U_f h_{t-1}+W_f x_t)
$$
$$
k_t = c_{t-1}\odot f_t
$$
Bramka dodająca¶
- definiowana przez cztery macierze: $U_g$, $W_g$, $U_i$, $W_i$
$$
g_t = tanh(U_g h_{t-1} + W_g x_t)
$$
$$
i_t = \sigma(U_i h_{t-1} + W_i x_t)
$$
$$
j_t = g_t \odot i_t
$$
Bramka wyjściowa¶
- definiowana jest przez macierze $U_o$, $W_o$
$$
c_t = k_t + j_t
$$
$$
o_t = \sigma(U_o h_{t-1} + W_o x_t)
$$
$$
h_t = o_t \odot tanh(c_t)
$$
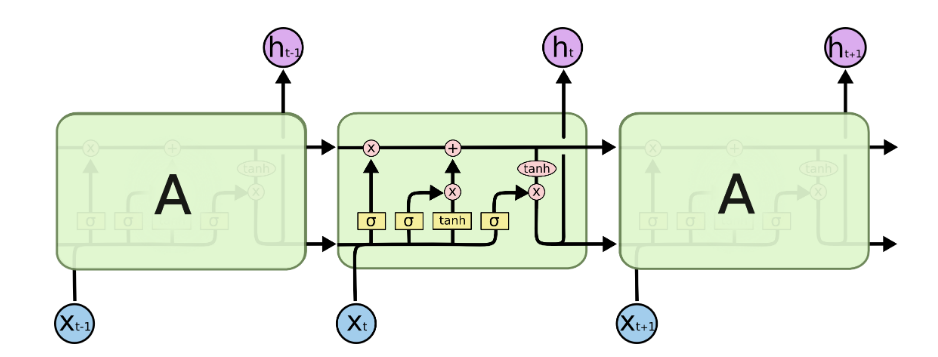
Plan¶
- Sztuczne sieci neuronowe
- Algorytm wstecznej propagacji błędu
- Sieci rekurencyjne
- Komórka LSTM
- Sieci transformacyjne
Przeuczenie modelu¶
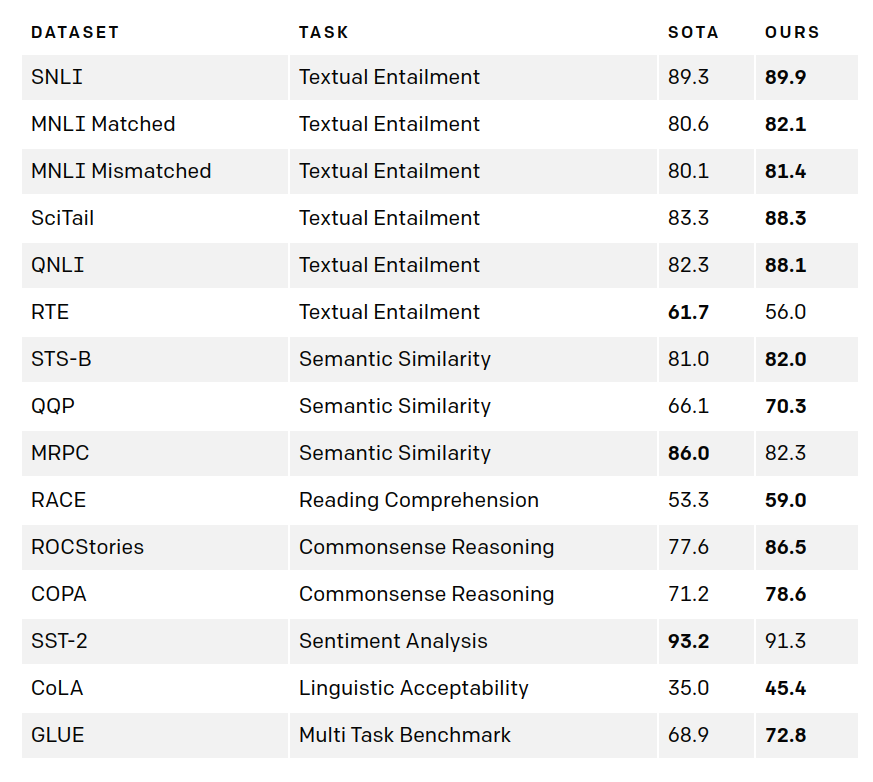
GPT-1 - OpenAI¶
GPT-2 - OpenAI¶

Źródło: "Language Models are Unsupervised Multitask Learners" A. Radford, J. Wu, R. Child, D. Luan,D. Amodei, I. Sutskever

In [2]:
%%html
<blockquote class="twitter-tweet"><p lang="en" dir="ltr">This is mind blowing.<br><br>With GPT-3, I built a layout generator where you just describe any layout you want, and it generates the JSX code for you.<br><br>W H A T <a href="https://t.co/w8JkrZO4lk">pic.twitter.com/w8JkrZO4lk</a></p>— Sharif Shameem (@sharifshameem) <a href="https://twitter.com/sharifshameem/status/1282676454690451457?ref_src=twsrc%5Etfw">July 13, 2020</a></blockquote> <script async src="https://platform.twitter.com/widgets.js" charset="utf-8"></script>
This is mind blowing.
— Sharif Shameem (@sharifshameem) July 13, 2020
With GPT-3, I built a layout generator where you just describe any layout you want, and it generates the JSX code for you.
W H A T pic.twitter.com/w8JkrZO4lk
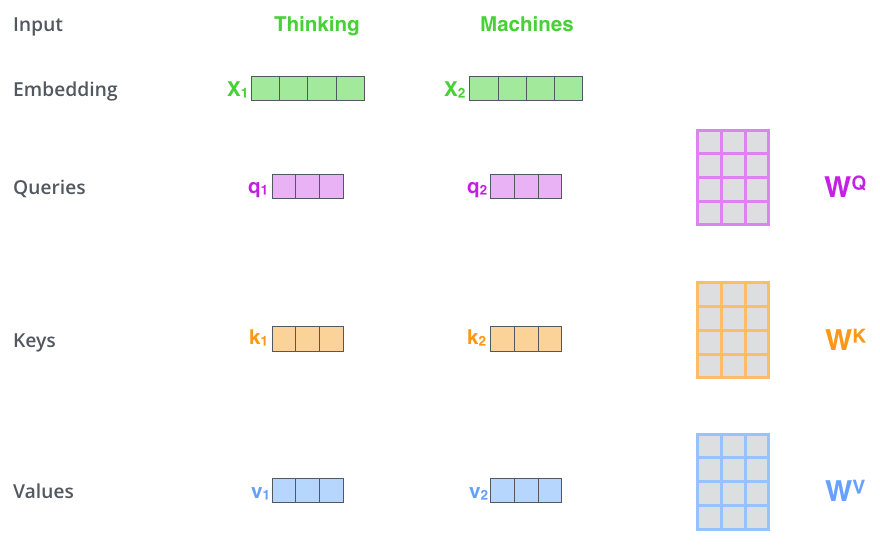
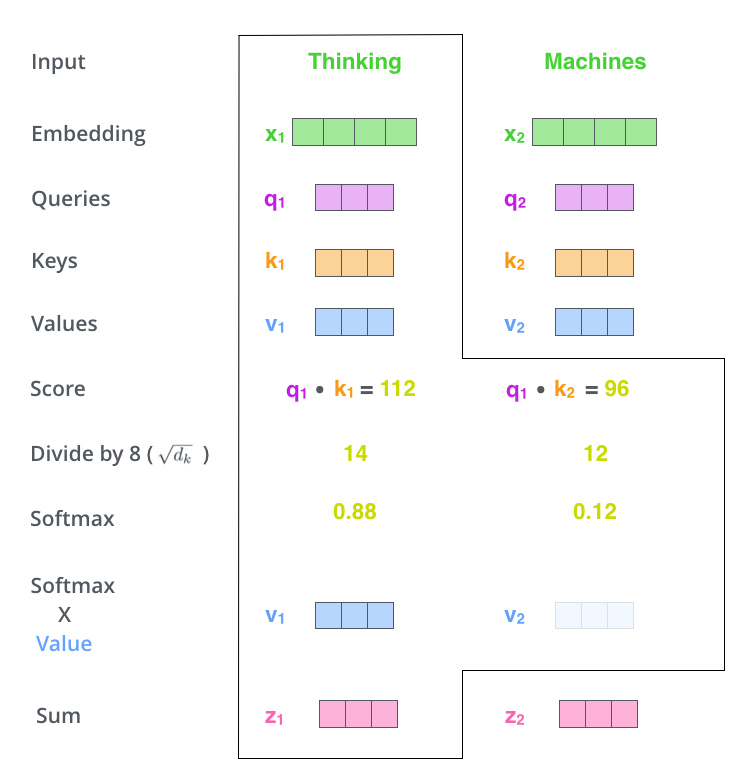
Istota mechanizmu samo-atencji¶
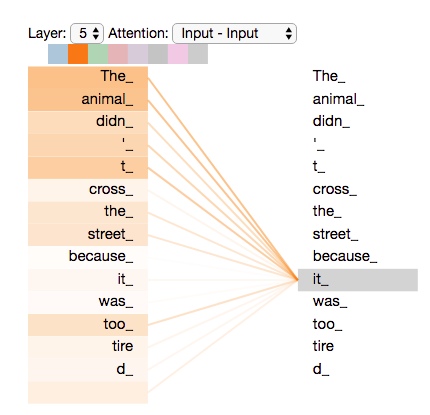
- The animal didn't cross the street because it was too tired.
- The animal didn't cross the street because it was too crowded.
In [1]:
%%html
<blockquote class="twitter-tweet"><p lang="en" dir="ltr">A demo of the attention mechanism of DeepMind's AlphaCode as it completes a coding question.<br><br>Now consider having 100s of browser tabs open and the attention corresponded to clicking on buttons and keyboard keys. <a href="https://t.co/mU0Cywm9N3">pic.twitter.com/mU0Cywm9N3</a></p>— dave (@dmvaldman) <a href="https://twitter.com/dmvaldman/status/1602326660220600324?ref_src=twsrc%5Etfw">December 12, 2022</a></blockquote> <script async src="https://platform.twitter.com/widgets.js" charset="utf-8"></script>
A demo of the attention mechanism of DeepMind's AlphaCode as it completes a coding question.
— dave (@dmvaldman) December 12, 2022
Now consider having 100s of browser tabs open and the attention corresponded to clicking on buttons and keyboard keys. pic.twitter.com/mU0Cywm9N3
Architektura transformacyjna¶
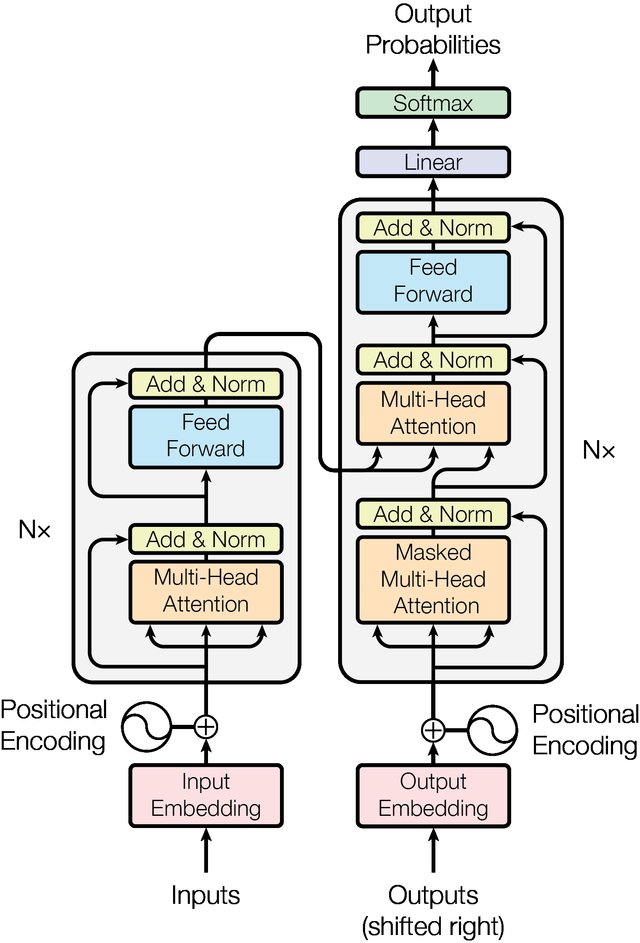
Implementacja wraz z wyjaśnieniem: https://threadreaderapp.com/thread/1470406419786698761.html
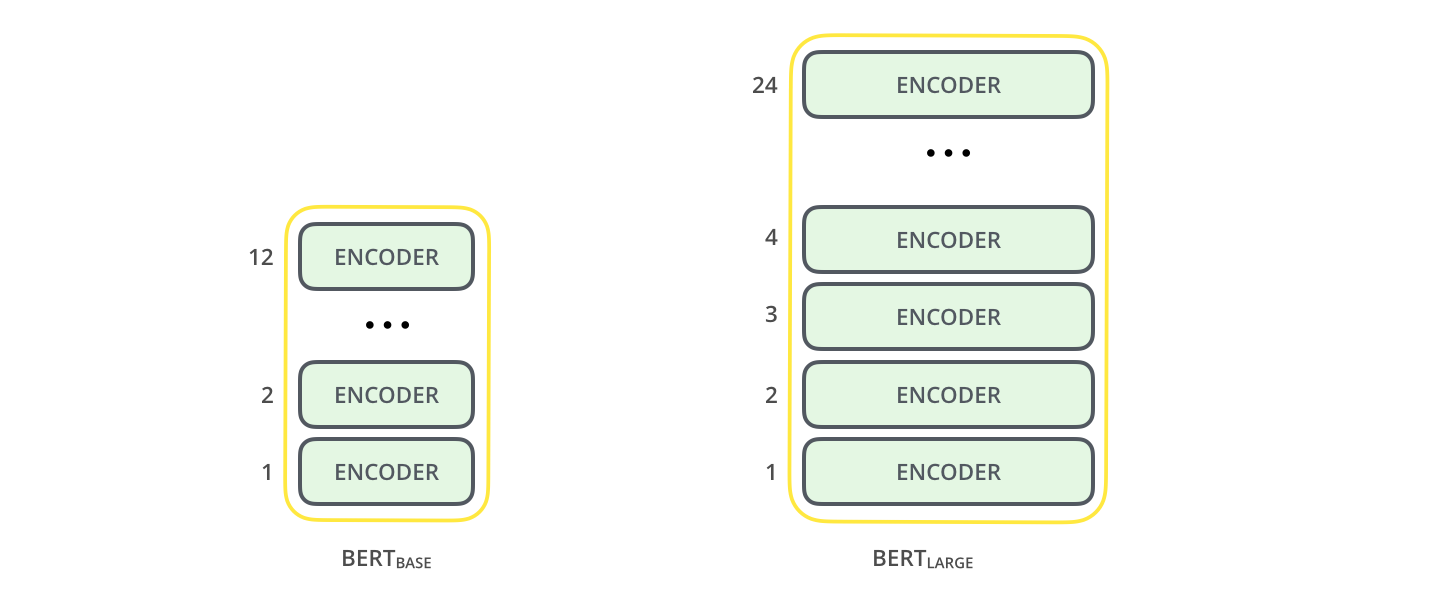
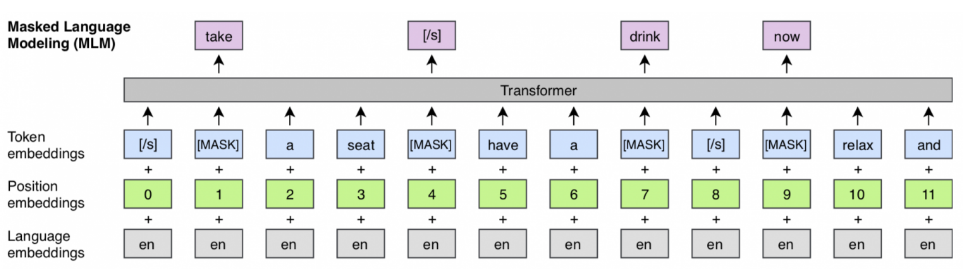
Warianty sieci transformacyjnych¶
- architekturalne
- BERT
- Albert
- XLNet
- BART
- GPT
- T5
- ...
- pretrenowane
- RoBERTa, XLMR
- FlauBERT
- FinBERT
- PolBERT
- HerBERT
- ...